W teorii zbiorów rozmytych możemy napotkać na zbiory, których uniwersum są liczby. O takich zbiorach mówimy, że są liczbami rozmytymi (lub nieostrymi). Zazwyczaj przyjmuje się, że te zbiory powinny być wypukłe i normalne.
Powyższe oznacza, że liczbą rozmytą nazwiemy zbiór rozmyty w uniwersum liczbowym M, który spełnia warunki:
[1]$$\forall x,y,z \in M, x<y<z: \: \: A(y)\geq A(x) \wedge A(z)$$ <– wypukłość
[2]$$\exists \: x \in M: \: \: A(x)=1$$ <– normalność
Warunki te potocznie możemy przełożyć na coś takiego:
Jeśli narysujemy nasz zbiór rozmyty na wykresie (tzn. jego funkcję przynależności) i zbiór nie będzie miejscami "zanikał" (tzn. wartość funkcji przynależności będzie rosnąć potem spadnie - czyli to jest ten "zanik" - a później znowu będzie rosnąć) oraz wysokość tego zbioru wynosi 1 (tzn. dla jakiegoś elementu z dziedziny wartość funkcji przynależności wynosi 1), to zbiór jest liczbą rozmytą.
W tym kursie będziemy przyjmować, że aby zbiór rozmyty był liczbą rozmytą musi spełniać warunek wypukłości oraz musi mieć uniwersum liczbowe. Miejscami będziemy pomijać warunek normalności - szczególnie wtedy, gdy będziemy mieli zbiory zapisane w notacji singletonowej.
Liczby rozmyte są wykorzystywane do modelowania nieprecyzyjnych danych liczbowych.

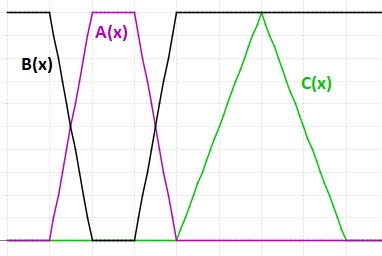
Spróbuj narysować te zbiory i zobacz, które miejscami "zanikają" ;)